
Next all you need to do is decide the maximum and minimum tide heights and scale the graph accordingly. You'll notice that you have low tides and high tides as normal but every so often you have super high and super low tides!
#MOON PLANET INFLUENCE OCEAN TIDE GRAPH PLUS#
You can plot this for time, now draw a third line which is moon A's force plus moon B's force. The high tides on any given day are the cumulative force from the moons.įor the sake of argument let's say moon A has a force of 10 and a period of 10 days, moon B has a force of 15 and a period of 15 days. You can represent this very easily as a graph with two sine waves on it. So you've got two moons of different masses orbiting at different periods. After all the planets in the solar system orbit on the same plane and it keeps the maths easier. Next you need to determine whether both moon are on the orbital plane, I would suggest they are. This means each moon can be independent to each other. The first thing to establish is whether the moons would have to have the same orbital period (do they both take either same amount of time to orbit the planet?) the answer is no, Europa has an orbital period of 85 hours and Ganymede of 172 hours. However, we can come up with a rough approximation which will at least help us get a feel for how the tides would work. In reality calculating tides is VERY complicated, it depends on many factors involving river emptying into the sea, the terrain around the shore, currents, weather etc. To do this plot each moon as a function of Time and manipulate the gravity of the moon by changing the amplitude and the orbital period by multiplying the time variable.Ī final plot showing the summation of the others gives the resulting forces on the tides. The stresses induced in the earth by an extraterrestrial mass are proportional to the gravitational field gradient dg( r ) / dr and NOT to the gravitational field g( r ).You can model the effect of two moons by summing two sine waves. The relative amount of influence is proportional to the objects mass, and inversely proportional to the third power of its distance from the earth. The moon, sun, and other planets have an influence on the earth in the form of perturbations (small changes) to the gravitational field. There have also been some small but significant correlations reported between the semi-diurnal tides and the rate of occurrence of aftershocks in some volcanic regions, such as Mammoth Lakes.
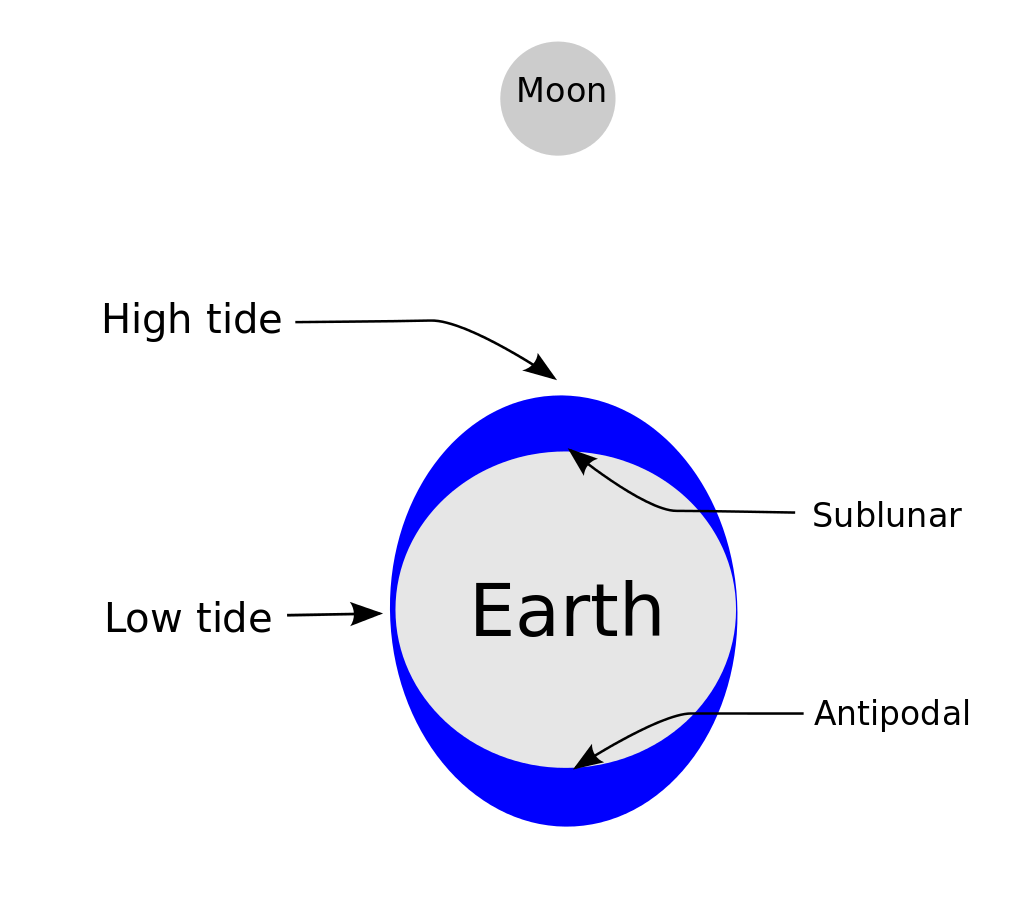
But you must stop and realize that the background probability is, in general, very low in a given place and year (fractions of a percent), so that raising this tiny probability by a factor of 3 during high tides still results in a very tiny probability. The increased probability is a factor of ~3 during high tides. When the confining pressure is lessened, the faults are unclamped and more likely to slip.
#MOON PLANET INFLUENCE OCEAN TIDE GRAPH FULL#
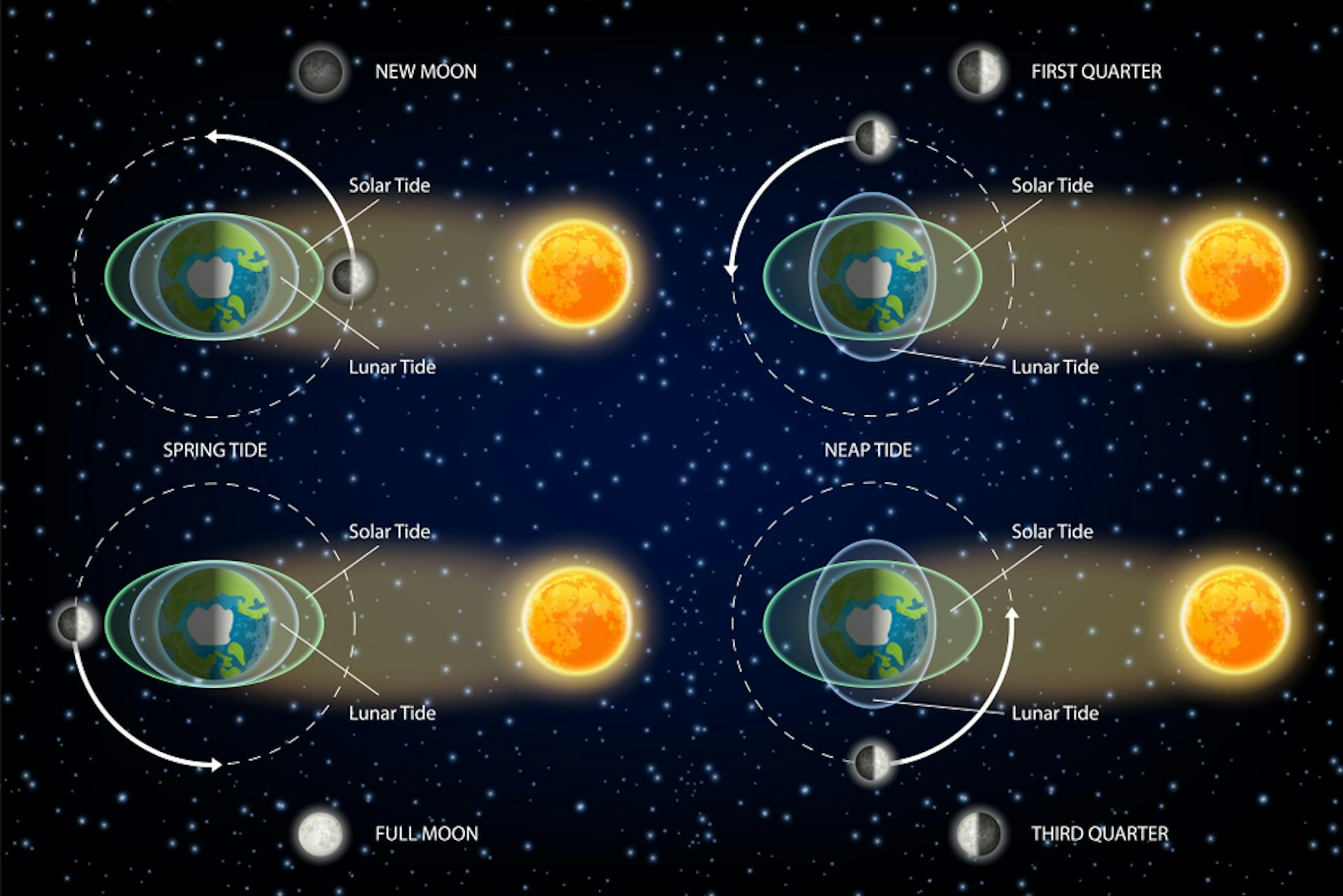
Lunar or solar eclipses represent, of course, special cases of full and new moon, but do not cause any special or different tidal effects from full and new moon.Įarth tides (Earth's surface going up and down by a couple of centimeters) and especially ocean tides (surface of the ocean going up and down by a meter or more) raise and lower the confining pressure on shallow, dipping faults near continental edges and in subduction zones. One study, for example, concludes that during times of higher earth and ocean tides, such as during times of full or new moon, earthquakes are more likely on shallow thrust faults near the edges of continents and in (underwater) subduction zones. Several recent studies, however, have found a correlation between earth tides (caused by the position of the moon relative to the earth) and some types of earthquakes. Many studies in the past have shown no significant correlations between the rate of earthquake occurrence and the semi-diurnal tides when using large earthquake catalogs. Earthquakes are equally as likely to occur in the morning or the evening.


 0 kommentar(er)
0 kommentar(er)
